Megújuló anyagok és folyadékok diffúziós folyamatainak energetikai kutatása
További információ, kapcsolat: Dr. Poós Tibor, poos@mail.bme.hu
Posztdoktori munkám során három, egymáshoz kapcsolódó kutatási témát indítottam el. Hő- és anyagátadás témakörében egyik esetben a folyadékok párolgási jelenségének matematikai leírását dolgoztuk ki, másik esetben a szemcsés anyagok fluidizációs szárítására jellemző térfogati hőátadási tényezőt meghatározó egyenletet, valamint a szárítást leíró matematikai egyenletrendszert alkottuk meg. Harmadik esetben a doktori munkám folytatásaként, egy berendezésben keveredő szemcsehalmaz mozgásállapotát, kinetikáját vizsgáltuk a szárítás és a keveredés hatékonyságának növelése, valamint a készülék energiafelhasználásának csökkentése érekében.
1;
A természetes áramlás által előidézett folyadék párolgásának vizsgálatára egy mérőállomást készítettünk, annak érdekében, hogy a szakirodalomban található párolgási sebesség számítására létrehozott összefüggések megbízhatóságát ellenőrizni lehessen. Méréseink során vizet párologtattunk. A szakirodalomban számos összefüggést közöltek, melyek a természetes áramlás során bekövetkező párolgás sebességét írják le. Ezek közül csak azokat értékeltük ki, melyek az adott mérési körülmények és feltételek mellett voltak érvényesek. A mérési eredményeinket ezeknek az egyenleteknek a megoldásaival hasonlítottuk össze. Az eredmények kiértékelése során négy egyenlet volt ±10%-os eltérésén belül a mért eredményekhez képest, míg akadtak olyan eredmények is, ahol akár 80%-os különbséget is meg lehetett figyelni. Megállapítható, hogy a párolgás jelenségének leírására még mindig nem létezik egy egzakt és biztonsággal használható összefüggés.
A kényszerített áramlás által előidézett párolgás vizsgálatára szintén egy erre alkalmas mérőberendezést használtam a kutatásom során. A hő- és anyagáramok irányainak szempontjából öt esetet különböztetünk meg. Az első két esetben a hőmérséklet különbség hajtóerő indukálja a diffúziót, míg a harmadik esetben, mikor a levegő és a folyadék hőmérséklete megegyezik, a nedvességtartalom különbség a hajtóerő. A negyedik esetben is fellép diffúzió, de mivel a folyadékfelszín hőmérséklete alacsonyabb a harmatponti hőmérsékletnél, ez nedvesség lecsapódás, kondenzáció formájában történik. Az ötödik esetben nem történik anyagátadás, mivel a levegő és a folyadék hőmérséklete megegyezik, illetve a levegő és a vízfelszín között nincsen parciális nyomáskülönbség, azok egyensúlyban vannak. Ezen öt esetből a kutatásom során eddig az első háromra végeztem méréseket a párolgás mérőállomáson vízre és acetonra. A víz és aceton esetén is ugyanazok a tendenciák figyelhetők meg, de a következőkben az acetonra kerülnek bemutatásra az eredmények. Az 1. ábra/a-c mutatja be a folyadék hőmérséklet, mind pedig a gáz hőmérséklet és sebesség változtatásának hatását a párolgási sebességre, ahol az elpárolgott aceton mennyiség van ábrázolva az idő függvényében. Megfigyelhető az 1. ábra/a, hogy a várakozásoknak megfelelően a nagyobb légsebesség nagyobb párolgási sebességet eredményezett, hiszen annál hamarabb került friss, száraz levegő a nedvességgel telített levegő helyére a folyadék felszínén. Az 1. ábra/b a folyadék hőmérséklet hatása került ábrázolásra, amiből kitűnik, hogy azonos légsebesség és levegő hőmérséklet mellett az aceton hőmérsékletének növelése a párolgási sebesség növekedését eredményezi. Az 1. ábra/c látható az az érdekes tendencia, hogy a gáz hőmérsékletének növekedése a párolgási sebesség csökkenését okozza, amit a folyadék felületére nehezedő egyre nagyobb vízgőz parciális nyomás okoz, ahogy növeljük a levegő hőmérsékletét. Az 1/d-f ábrák mutatják a hőáram iránya szerinti megkülönböztetést az egyes esetekre. Az összehasonlításukból látható, hogy a legnagyobb párolgási sebesség akkor adódik, amikor a hőáram iránya megegyezik az anyagáram irányával, azaz a folyadékból a levegőbe irányul. Az 1. ábra/d és f diagramok esetében is jellemző a tendencia, hogy magasabb folyadék hőmérséklet nagyobb párolgási sebességet eredményez. Az 1. ábra/f látható, hogy ha nincs hőáram a két fázis között, akkor a közös hőmérséklet befolyásolja a párolgási sebességet, vagyis nagyobb hőmérséklet nagyobb párolgási sebességet eredményez. Ez azért lehetséges, mert a hőmérséklet növekedésével az aceton párolgáshője csökken, a nedvességtartalomkülönbség hajtóerő pedig nő.
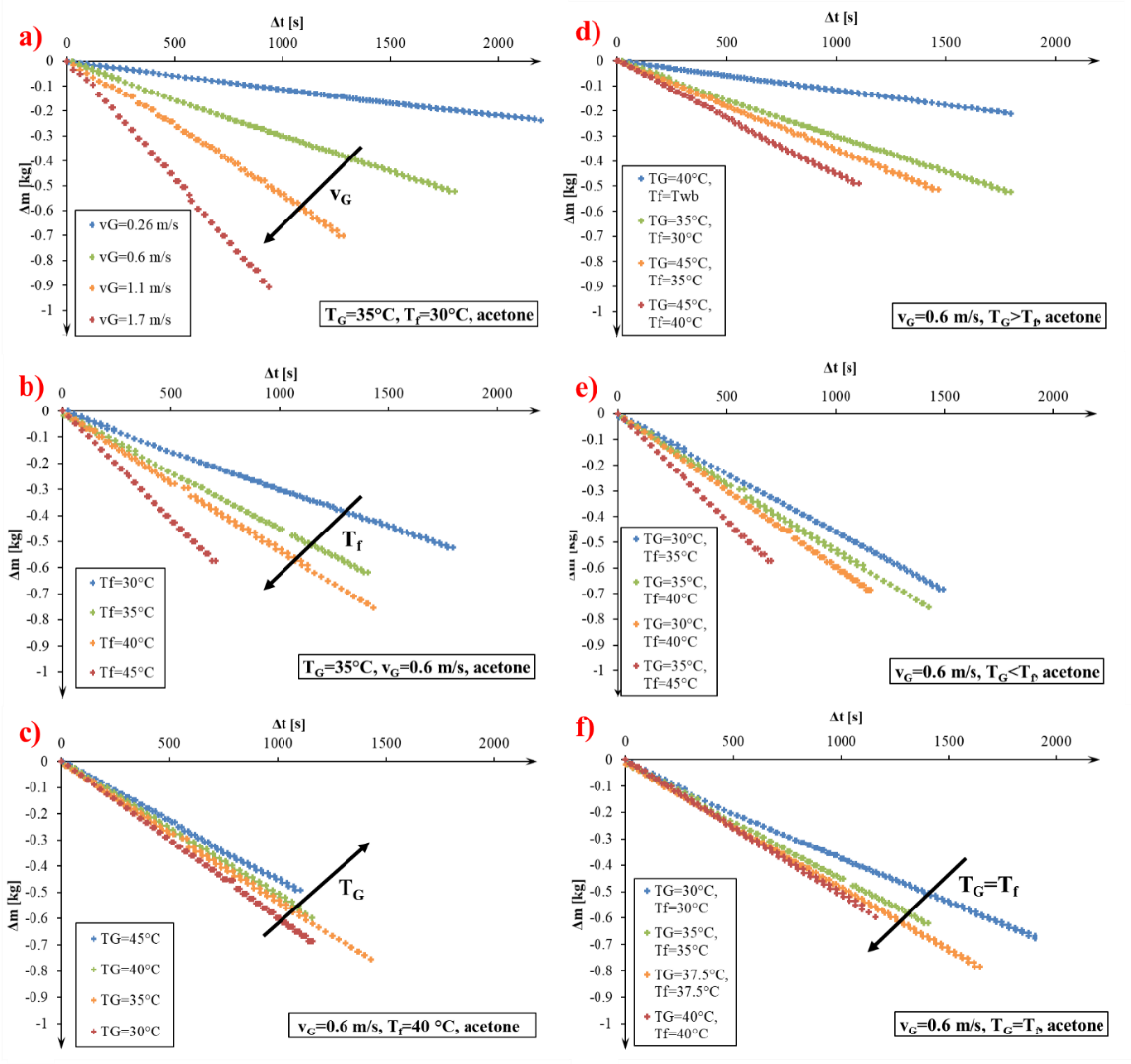
1. ábra. Az elpárolgott aceton mennyisége az idő függvényében ( a) A légsebeség hatása, b) A folyadék hőmérséklet hatása, c) A gáz hőmérsékletének hatása, d-f) A hőáram irányának hatása)
A mérési eredményeket felhasználva egy Sherwood- és Reynolds-szám közötti dimenziótlan összefüggést hoztunk létre a párolgás jelenségének leírására, a külön vizsgált három esetre, ami a 2. ábrán látható. Ezen egyenletek segítségével megbecsülhető a párolgási sebesség, ha ismert a közegek hőmérséklete és a párolgó felület nagysága.
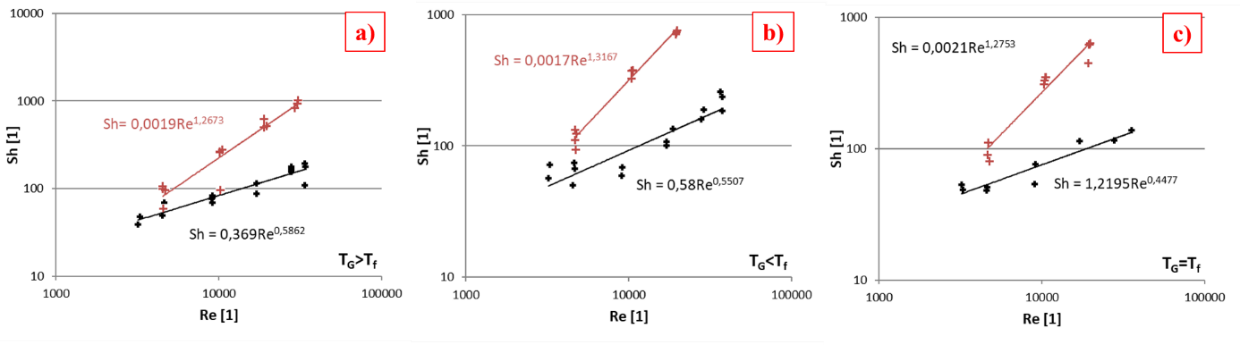
2. ábra. A Sherwood- és Reynolds-szám közötti kapcsolat párolgás víz (fekete) és aceton (piros) esetén a hőáram irányától függően ( a) A gáz hőmérséklet magasabb, mint a folyadék hőmérséklet, b) A gáz hőmérséklet alacsonyabb, mint a folyadék hőmérséklet, c) A két közeg hőmérséklete megegyezik)
2;
Szemcsés anyagok fluidizációs szárításának modellezésével foglalkozó szakirodalmak áttekintése után megállapítottuk, hogy számos szerző foglalkozik a hő- és anyagátadási viszonyok leírásával. A szakirodalomban bevett gyakorlattól eltérően a hőátadási tényezőt az érintkezési felülettel összevonva ún. térfogati hőátadási tényező bevezetését javasoltuk, kiküszöbölve az érintkezési felület meghatározásában rejlő bizonytalanságot. Kutatásunk során méréseket végeztünk egy félüzemi fluidizációs szárítón, széles hőmérséklet- és levegősebesség tartományokban. A mérőállomást korábbi munkánk keretében terveztük és üzemeltük be a Tanszék laboratóriumába. A mérési módszer további fejlesztésével meghatározhatókká váltak a térfogati hőátadási tényezők a szárítás állandó és csökkenő száradási sebesség szakaszán.
A méréseket különböző típusú mezőgazdasági és élelmiszeripari szemestermékekkel végeztük el, szakaszos üzemmódban. A mérések során meghatároztuk a térfogati hőátadási tényező értékét a szemcsés ágy és a szárítógáz között a szárítás teljes tartományán. Az eddigi mérési eredmények és szakirodalmi források felhasználásával dimenziótlan függvénykapcsolatot hoztunk létre a térfogati hőátadási tényező meghatározására a szárítás állandó száradási sebességű tartományán, adott értelmezési tartományban. A mérési eredményekkel és a szakirodalmi értékek átdolgozásával létrehozott kriteriális egyenlet a 3. ábrán látható, mely adott Reynolds-szám tartományban (17 < Re < 1154) érvényes.
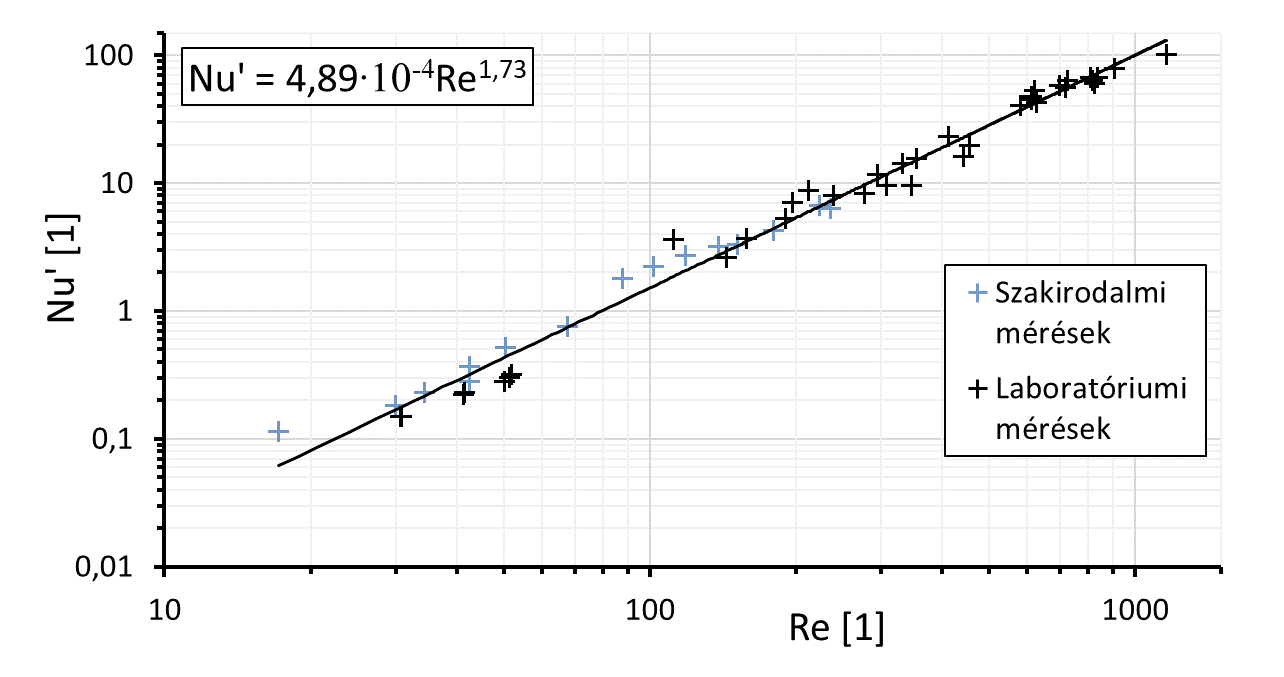
3. ábra. Nu’ – Re összefüggés a mérési és szakirodalmi eredményekből
Kidolgoztuk a fluidizációs szárításra vonatkozó hő- és anyagátadást leíró matematikai modellt a térfogati hőátadási tényező felhasználásával. A modell alkalmas a száradó anyag hőmérsékletének, nedvességtartalmának, valamint a szárítógáz hőmérsékletének és abszolút nedvességtartalmának idő szerinti, továbbá a szárítógáz hőmérsékletének és abszolút nedvességtartalmának a berendezés magassága menti változásának leírására. A matematikai modell bemenő paraméterei a szárítási jellemzőkön és a geometriai adatokon kívül a térfogati hőátadási tényező. A matematikai modell felhasználásával számítási algoritmus készült, mely alkalmazásával a bemeneti paraméterek megadása után meghatározhatóvá válik a szükséges tartózkodási idő adott szemcsés anyag kívánt nedvességtartalomra történő szárításánál.
Ezen felül számíthatóvá válik a szemcsék és a szárítógáz közötti szükséges szárítási hossz, mely magasság mentén az együttes hő – és anyagátadás megtörténik. A szárítógáz a berendezésbe belépve felveszi a nedvességet a száradó anyagból, majd bizonyos magasságban megközelíti a telítési értéket, melynél a nedvességdiffúzió jelentősen lelassul. A modell segítségével számolható a levegő abszolút nedvességtartalma és hőmérséklete a szárító magassága mentén. A 4. ábrán a hőmérséklet és nedvességtartalom profilok láthatók a szárító magassága mentén. A 4. ábra/a a hőmérséklet alakulását mutatja a szárítótér mentén. Az ábrán szürke vonal jelzi a telítési hőmérsékletet . A szárítási hossz azon a magasság koordinátán van értelmezve, ahol a szárítógáz hőmérséklete 1 °C-kal megközelíti a telítési hőmérsékletet. Ebben az esetben a szárítási hossz 175 mm volt, mely pontozott vonallal van jelölve. A szárítógáz abszolút nedvességtartalma a szárítási hossz ismeretében határozható meg, 4. ábra/b az abszolút nedvességtartalom profilt mutatja be a szárító hossza mentén. Ez azt jelenti, hogy a szemcsék és a szárítógáz közötti hő- és anyagátadás a szárító egy kis részében van jelen, efölött a levegő telítődik és nem képes több nedvességet magával ragadni, illetve a hőátadás sem számottevő.
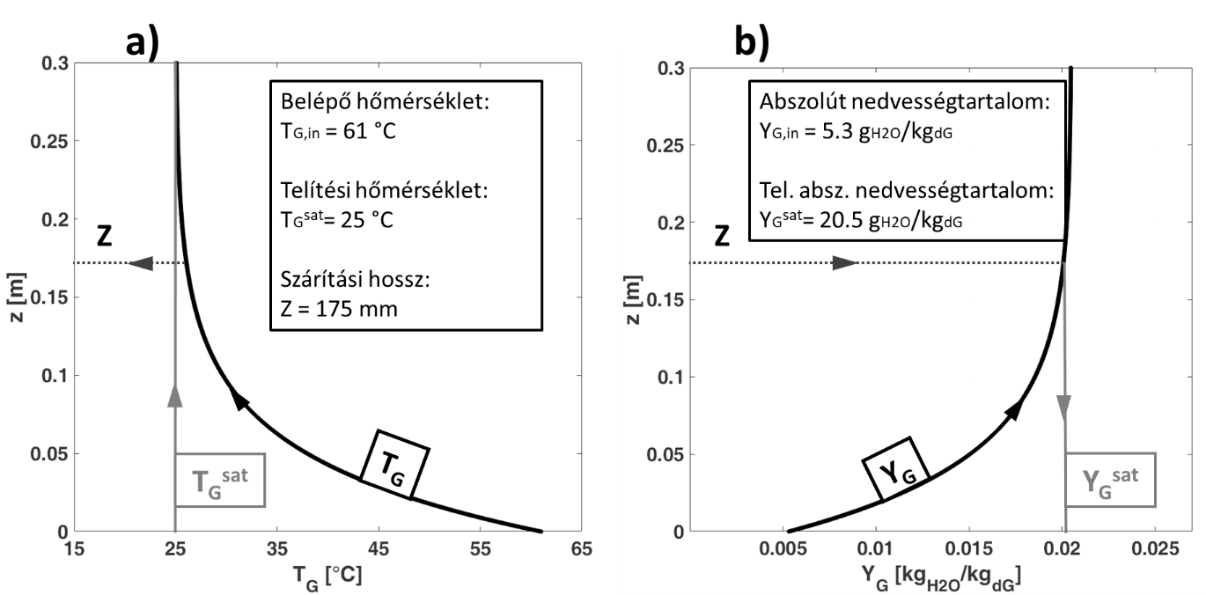
4. ábra Szárítógáz hőmérséklet (a) és abszolút nedvességtartalom (b) profilja a szárító magassága mentén
Továbbá a modell segítségével kiszámítható a szárítógáz hőmérséklete és abszolút nedvességtartalma az állandó száradási sebességű szakaszon z=Z koordinátán. A nedves hőmérő hőmérséklet és az ehhez tartozó telítési abszolút nedvességtartalom Mollier-diagram segítségével határozható meg a szárítóba belépő levegő hőmérsékletének és nedvességtartalmának ismeretében.
A matematikai modellel számított és a telítési hőmérséklet közötti különbség minden esetben 0,9 °C alatt volt, az abszolút hőmérsékletek között pedig 1,5 gH2O/kgdG alatt. Továbbá a mért és a modellel számított értékek közötti különbség a hőmérsékletek esetében 0,8 °C, abszolút nedvességtartalmak esetén pedig 0,4 gH2O/kgdG alatt volt. A mérési és számítási eredmények közötti eltéréseket mérési pontatlanságokra is vissza lehet vezetni.
3;
Folyadékok keverési teljesítményigénye meghatározható empirikus módszerrel, melynek leírása a szakirodalom alapján jelenleg jól ismert. Azonban szilárd szemcsés anyagok keverési teljesítményének általános leírása a szakirodalomban jelenleg hiányosan kutatott terület, általános összefüggés nem ismert. Kutatásom célja szilárd szemcsés anyagok keverési teljesítményigényének meghatározása laboratóriumi mérésekkel és numerikus számításokkal. A keverési teljesítményigényt szilárd anyagok esetén befolyásolja a keverő geometriai kialakítása, az üzemi paraméterek (fordulatszám, töltési fok, kevert anyagtömeg), az anyag anyagjellemzői és nedvességtartalma (sűrűség, belső súrlódási szög, rugalmassági modulus, méret, kohézió). Szemcsés anyagok keverésének vizsgálatára egy félüzemi keverős dobszárítóban hajtottuk végre a méréseinket. Méréseinket hántolt kölessel végeztük a keverőelem fordulatszámának, töltési fok, anyag nedvességtartalom értékeinek változtatásával. Az eredmények alapján megállapítható, hogy a dob töltési fokának a növelésével nőtt a keverési teljesítményszükséglet, mivel a keverőelem több anyagot, azaz nagyobb tömeget mozgatott. Továbbá az a fordulatszám növelése esetén másodfokú polinomiális jelleggel növekedett, mely megegyezik a szakirodalomban leírt tapasztalatokkal. Viszont az anyag nedvességtartalmának növelése a keverési teljesítményigényt csak kis mértékben növelte. Továbbá nem a legnagyobb nedvességtartalom esetén lépett fel a legnagyobb teljesítményigény, melyet a szemcsék halmazsűrűségének csökkenése okozhatott, illetve a víz súrlódáscsökkentő hatása, amely könnyebben lehetővé teszi a köles szemcsék egymáson történő elforgását, elmozdulását.
Numerikus vizsgálatok végrehajtásához python programozási nyelven megépítésre kerültek a rézsűszög mérőállomás és a direkt nyíródobozos berendezés diszkrételemes modelljei a Yade nyílt forráskódú szoftver alkalmazásával. A mérési eredményekkel történő validálással kalibráltuk a hántolt köles mikromechanikai kohézióját, mely a keverős berendezés dinamikus szimulációjához szükséges. A vizsgált keverési folyamat diszkrételemes modelljét az 5. ábra szemlélteti.

5. ábra. A vizsgált keverési folyamat diszkrételemes modelljének lépései. (1. szemcsék generálása, 2. halmaz ülepítése, 3. ülepített szemcsehalmaz, 4. kevert szemcsehalmaz)
A keverési teljesítményszükséglet a nyomaték és a fordulatszám ismeretében számításra került. A mérési és a szimulációs eredmények összehasonlítása a 6. ábrán láthatók.
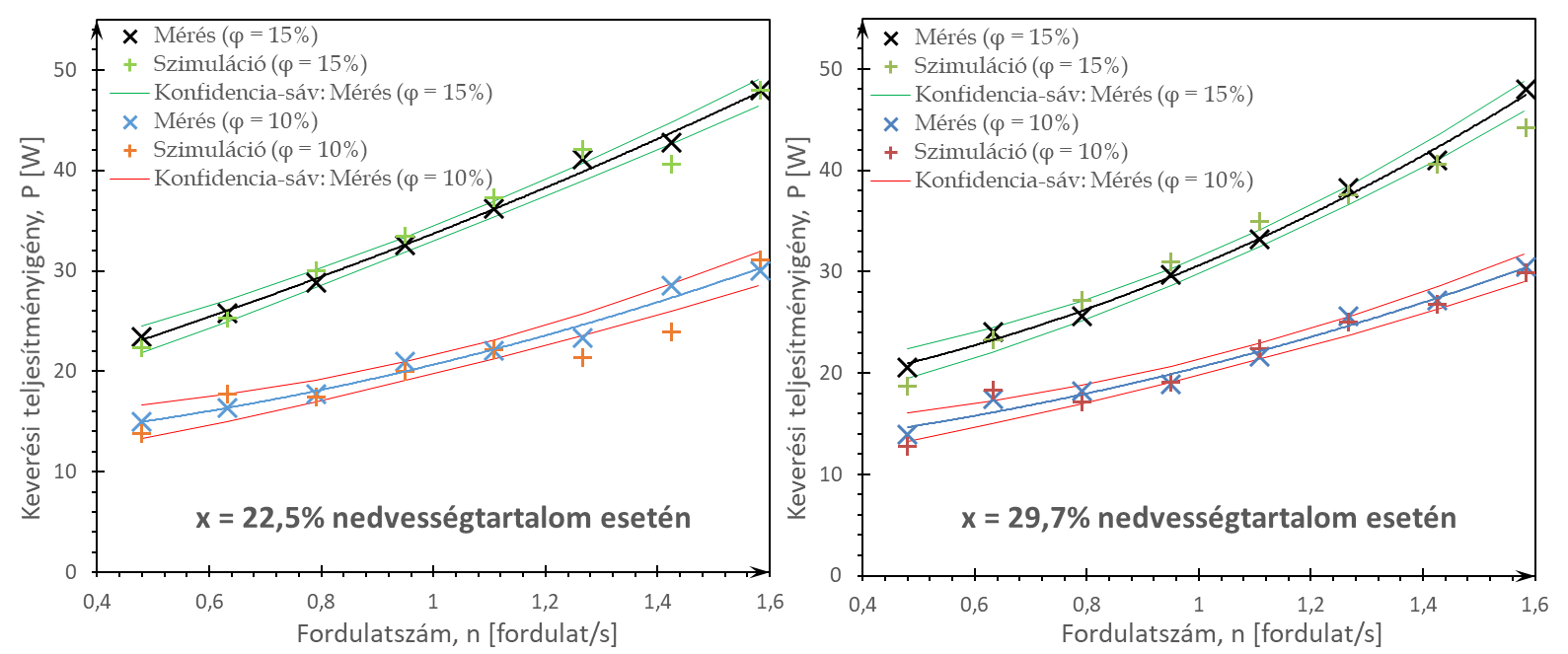
6. ábra. x=22,5% és x=29,7% nedvességtartalomú hántolt köles mért és szimulált keverési teljesítményigénye (P) a keverő fordulatszámának (n) függvényében 10% és 15% töltési fok esetén (φ), 99% valószínűségi szintű konfidencia-sávokkal
A 22,5% nedvességtartalom esetén a szimulációval kapott kiugró pontok jellemzően a konfidencia sávok alá, míg 29,7% nedvességtartalom esetén azok fölé estek. Statisztikai módszerekkel (relatív eltérés, konfidencia-sáv, regresszió analízis) megállapítottuk, hogy a szimulációk megfelelő pontossággal közelítették a laboratóriumi mérések eredményeit. Továbbá a felépített diszkrételemes keverős modell a hántolt köles mért és kalibrált mikromechanikai anyagparamétereivel alkalmas a félüzemi keverős dobszárító keverési teljesítmény értékeinek meghatározására. A felépített modellel további nedvességtartalmakon meghatározható a keverési teljesítményigény, így csökkentve a költséges, energia- és munkaigényes laboratóriumi méréseket. Továbbá a hántolt köles keverése során fellépő homogenizáció vizsgálata is lehetővé válik a kutatás további szakaszában.
A projekt összegzéseként az alábbi eredmények foglalhatóak össze:
· A párolgás jelenségének vizsgálata során célunk a párolgási sebesség meghatározására alkalmas összefüggés bevezetése volt, mely során adott körülmények között meghatározható adott időegység alatt elpárolgott folyadék mennyisége egy tározóból.
· A fluidizációs szárítás témakörét illető elméleti és gyakorlati kutatások eredményeit felhasználva lehetővé válik a fluidizációs szárítás folyamatának eddiginél pontosabb modellezése, mely segíti a különböző műveleti és geometriai tényezők hatásának elemzését, továbbá a szárítók hatékony üzemeltetését és gazdaságos tervezését.
· Szemcsés anyagok keverési teljesítményének eddigieknél pontosabb meghatározásával csökkenthető az energiaigény, továbbá hozzájárulhat a rendszer gazdaságos tervezéséhez.